Razones y proporciones
1- Razón
Una razón es una comparación entre dos o más cantidades. Puede expresarse mediante una fracción. Si las cantidades a comparar son a y b, la razón entre ellas se escribe como:

Razón entre dos números
Siempre que hablemos de Razón entre dos números nos estaremos refiriendo al cociente (el resultado de dividirlos) entre ellos.
Entonces:
La razón entre dos números a y b cociente entre
|
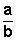
Por ejemplo, la razón entre 10 y 2 es 5 , ya que
|
Proporción numérica
Ahora, cuando se nos presentan dos razones para ser comparadas entre sí, para ver como se comportan entre ellas, estaremos hablando de una proporción numérica.
Entonces:
| Los números a, b, c y d forman una proporción si la razón entre a y b es la misma que entre c y d . es decir: 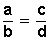
Los números 2, 5 y 8, 20 forman una proporción, ya que la razón entre 2 y 5 es la misma que la razón entre 8 y 20.
| |||
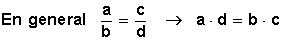
Ejemplo
Ejemplo
Un saco de papas pesa 20 kg. ¿Cuánto pesan 2 sacos?
Un cargamento de papas pesa 520 kg ¿Cuántos sacos de 20 kg se podrán hacer?
Número de sacos
|
1
|
2
|
3
|
...
|
26
|
...
|
Peso en kg
|
20
|
40
|
60
|
...
|
520
|
...
|
Ejemplo:
En una sala de clases hay 10 mujeres y 18 hombres. ¿Qué relación numérica existe entre el número de mujeres y el número de hombres?
La relación entre el número de mujeres y el número de hombres es de "10 es a 18" , otra forma de leerlo es "10 de 18 "
El término a es el antecedente de la razón y el b, el consecuente.

El resultado de la división o cociente entre el antecedente y el consecuente se denomina valor de la razón

Dos o más razones son equivalentes cuando tienen igual valor.
2- Proporciones
Una proporción es la igualdad de dos razones.

2.1- Propiedad fundamental
En toda proporción, el producto de los términos medios es igual al producto de los términos extremos (Teorema fundamental de las proporciones). Es decir:

Ejemplo:
Si tenemos la proporción:

Y le aplicamos la propiedad fundamental señalada queda:
3 • 20 = 4 • 15, es decir, 60 = 60
Esta es la propiedad que nos permite detectar si dos cantidades presentadas como proporción lo son verdaderamente.
https://www.portaleducativo.net/septimo-basico/293/Razones-proporciones
Proporción directa
Cuando dos cantidades están relacionadas de tal forma que cuando una cantidad crece la otra también crece el mismo número de veces, entonces tenemos una proporción directa.
Ejemplo 3
Un paquete con 600 ml de refresco cuesta $5.00 pesos. ¿Cuánto cuesta un litro de ese refresco?
Sabemos que 600 ml de refresco cuestan $5.00 pesos.
La sexta parte de 600 ml debe costar la sexta parte de $5.00 pesos.
Es decir, 100 ml de ese refresco deben costar $5.00/6 pesos.
Un litro de refresco equivalen a 1,000 ml, y 1,000 ml equivalen a 10 veces 100 ml.
Entonces, 1 litro de ese refresco debe costar 10 veces más que lo que cuestan 100 ml.
Esto es, 1 litro de ese refresco cuesta: pesos.
pesos.
La sexta parte de 600 ml debe costar la sexta parte de $5.00 pesos.
Es decir, 100 ml de ese refresco deben costar $5.00/6 pesos.
Un litro de refresco equivalen a 1,000 ml, y 1,000 ml equivalen a 10 veces 100 ml.
Entonces, 1 litro de ese refresco debe costar 10 veces más que lo que cuestan 100 ml.
Esto es, 1 litro de ese refresco cuesta:
Ejemplo 4
Un vendedor de Hot Dogs puede preparar 20 Hot Dogs en 30 minutos. ¿Cuántos puede preparar en 45 minutos?
Nosotros sabemos que puede preparar  hot dogs en
hot dogs en  minutos.
minutos.
Entonces puede preparar el doble de hot dogs en el doble de tiempo. Y debe preparar la mitad de hot dogs en la mitad del tiempo.
Eso significa que puede preparar hot dogs en la mitad de 30 minutos, es decir, en
hot dogs en la mitad de 30 minutos, es decir, en  minutos.
minutos.
Entonces, si sumamos lo que puede preparar en 30 minutos con lo que puede preparar en 15 minutos, obtenemos lo que puede preparar en 45 minutos.
En conclusión, puede preparar hot dogs en 45 minutos.
hot dogs en 45 minutos.
Entonces puede preparar el doble de hot dogs en el doble de tiempo. Y debe preparar la mitad de hot dogs en la mitad del tiempo.
Eso significa que puede preparar
Entonces, si sumamos lo que puede preparar en 30 minutos con lo que puede preparar en 15 minutos, obtenemos lo que puede preparar en 45 minutos.
En conclusión, puede preparar
Ejemplo 5
En un asilo se consumen 14 kg de harina por semana (7 días). ¿Cuántos kilogramos de harina se consumen en 30 días?
En la séptima parte del tiempo se consume la séptima parte de kilogramos de harina.
Esto significa que en un día se consumen 2 kilogramos de harina.
En 30 días se consumen 30 veces más de harina que lo que se consume en un día,
Esto indica que en 30 días se consumen kilogramos de harina.
kilogramos de harina.
Esto significa que en un día se consumen 2 kilogramos de harina.
En 30 días se consumen 30 veces más de harina que lo que se consume en un día,
Esto indica que en 30 días se consumen
NOTA:Dos magnitudes son directamente proporcionales cuando, al multiplicar o dividir una de ellas por un número cualquiera, la otra queda multiplicada o dividida por el mismo número.
2- Proporcionalidad directa
Dos cantidades son directamente proporcionales si al aumentar o disminuir una de ellas, la otra aumenta o disminuye, respectivamente, en la misma razón.
Ejemplo:
- Indica si las variables son directamente proporcionales
a. La medida del lado de un cuadrado y su perímetro:
Respuesta Sí, porque a mayor longitud de sus lados mayor perímetro. (si una variable aumenta la otra aumenta en la misma razón).
b. El número de trabajadores y los días que se demoran en hacer un trabajo, si todos trabajan de igual manera: Respuesta: No, porque a mayor cantidad de trabajadores menos cantidad de días. (si una variable aumenta, la otra disminuye en la misma razón).
c)Juan ha utilizado 20 huevos para hacer 4 tortillas iguales. ¿Cuántos huevos necesita para hacer 6 tortillas? ¿Y para hecer 2?
EJEMPLO DE PROPORCIONALIDAD DIRECTA
REGLA DE TRES SIMPLE DIRECTA
Ejemplo 1
En 50 litros de agua de mar hay 1.300 gramos de sal. ¿Cuántos litros de agua de mar contendrán 5.200 gramos de sal?
Como en doble cantidad de agua de mar habrá doble cantidad de sal; en triple, triple, etc. Las magnitudes cantidad de agua y cantidad de sal son directamente proporcionales .
Si representamos por x el número de litros que contendrá 5200 gramos de sal, y formamos la siguiente tabla:
Litros de agua
|
50
|
x
|
Gramos de sal
|
1.300
|
5.200
|
Se verifica la proporción:
|
Y como en toda proporción el producto de medios es igual al producto de extremos (en palabras simples, se multiplican los números en forma cruzada) resulta:
50 por 5.200 = 1.300 por x
Es decir
|
3- Proporcionalidad inversa
Dos cantidades son inversamente proporcionales si una de ellas aumenta, la otra disminuye en la misma razón .
Ejemplos:
Indica si las variables son inversamente proporcionales.
a) El número de albañiles y el tiempo empleado en hacer el mismo edificio.
Respuesta: Son inversamente proporcionales, ya que con el doble, triple... número de albañiles se tardará la mitad, tercera parte de tiempo en construir el mismo edificio.
b) La velocidad de un auto y el trayecto recorrido en el mismo tiempo.
Respuesta: No es inversa ya que a tiempo constante, con el doble o el triple... de la velocidad, el auto recorrerá el doble, triple... de espacio.
c) La velocidad de un auto y el tiempo empleado en recorrer el mismo trayecto.
Respuesta: Son inversamente proporcionales, ya que, a espacio constante, con el doble, triple... velocidad, el auto tardará la mitad, tercera parte... de tiempo en recorrerlo.
ACTIVIDAD DE RECUPERACIÓN-resolver los siguientes problemas
1) Si 5 m de tela valen $8500, ¿cuánto valen 8 m?
2) Veinte alumnos hicieron una excursión y consumieron 15 botellas de jugo. ¿Cuántas botellas de jugo se habrían consumido, si hubieran ido los 50 alumnos del curso?
3) Con el dinero que tengo, puedo comprar 20 chocolates a $ 20 cada uno. Si los chocolates suben a $ 25, ¿cuántos podré comprar? R: puede comprar 16 chocolates
4)Dos trabajadores tardan 32 horas en pintar una casa. ¿Cuántos trabajadores se requieren para que realicen la tarea en 4 horas?
5) En un viaje, 300 personas requieren de 975 litros de agua para consumo (elaboración de alimentos y bebidas) durante un día. Si hacemos caso del dicho: “una persona necesita de dos litros de agua diarios”, ¿para cuántas personas alcanzará el agua?
6) José marca 5 goles cada 25 minutos de partido. Calcular mediante una regla de tres cuántos goles marcará en una hora. Indicar si es una proporcionalidad directa o inversa.
7) Un autobús recorre 70km en dos horas. ¿Cuánto tardará en realizar un viaje de 345km? Indicar si es una proporcionalidad directa o inversa.
8) Si tardamos 3 horas en estudiar los 5 primeros temas del examen, ¿cuántas horas más necesitamos para terminar de estudiar si en total hay 17 temas?
9) Tres personas tardan 12 horas en pintar un muro. ¿Cuántas personas se necesitan si se quiere finalizar la tarea en tan solo 4 horas?
10) 100 litros de aceite cuestan $189.000 ¿Cuánto cuestan 125 litros del mismo producto?
BUENA SUERTE Y MUCHOS EXITOS
Bibliografía
1)https://www.portaleducativo.net/octavo-basico/806/Relacion-de-proporcionalidad-directa-2)inversahttps://www.aprendematematicas.org.mx/unit/razones-y-proporciones/
3) https://www.vitutor.com/di/p/a_5e.html
Escribir nombres y apellidos
ResponderEliminargrado