GEOMETRIA PARA 7 - TEOREMA DE PITAGORAS

EL TEOREMA DE PITAGORAS

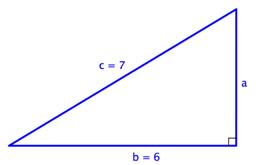
Teorema de Pitágoras.- En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

HIPOTENUSA:es el lado de mayor longitud de un triangulo rectángulo y siempre esta al frente del angulo del ángulo recto.

CATETOS:son los dos lados que forman el ángulo recto de un triangulo rectángulo











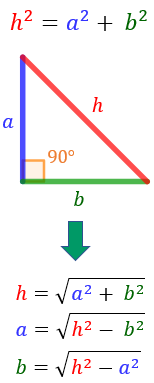
Hace mucho tiempo, un matemático Griego llamado Pitágoras descubrió una propiedad interesante de los triángulos rectángulos: la suma de los cuadrados de las longitudes de los catetos es igual al cuadrado de la longitud de la hipotenusa del triángulo. A esta propiedad — que tiene muchas aplicaciones en la ciencia, el arte, la ingeniería y la arquitectura — se le conoce como Teorema de Pitágoras.

Pitágoras estudió los triángulos rectángulos, y las relaciones entre los catetos y la hipotenusa de un triángulo rectángulo, antes de derivar su teoría.

Intentemos el Teorema de Pitágoras con un triángulo.

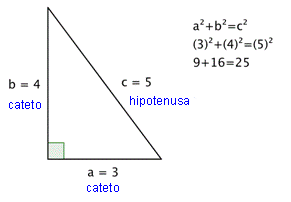
El Teorema de Pitágoras puede también representarse en términos de área. En un triángulo rectángulo, el área del cuadrado de la hipotenusa es igual a la suma de las áreas de los cuadrados de los catetos. Puedes ver la ilustración siguiente para el mismo triángulo rectángulo ,cuyos catetos miden 3  y 4 respectivamente,y la hipotenusa mide 5.

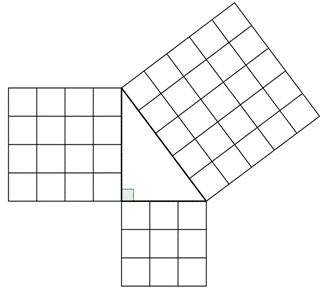
NOTA:Observa que el Teorema de Pitágoras sólo funciona para triángulos rectángulos.

Encontrar la longitud de la hipotenusa

Puedes usar el Teorema de Pitágoras para encontrar la longitud de la hipotenusa de un triángulo rectángulo si conoces la longitud de los otros dos lados del triángulo, llamados catetos. Puesto de otra manera, si conoces las longitudes de a y b, puedes encontrar c.

EJEMPLO:calcular la longitud de la hipotenusa en la siguiente grafica

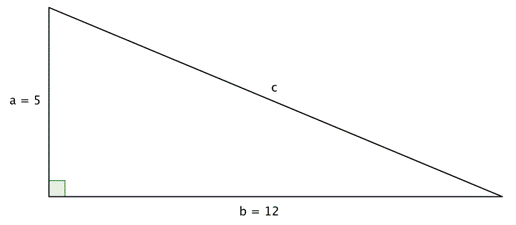
EJEMPLO

EJERCICIO:calcular la longitud del hilo que sostiene la cometa.

Encontrar la longitud de un cateto:Puedes usar la misma fórmula para encontrar la longitud del cateto de un triángulo si te proporcionan las medidas de la hipotenusa y del otro cateto. Considera el siguiente ejemplo.

GEOMETRIA PARA SEXTO-EL PLANO CARTESIANO

Plano Cartesiano

LLamado también Sistema Cartesiano de Coordenadas, está formado por dos rectas numéricas cortadas perpendicularmente; el punto de corte de estas rectas es el origen o cero y a partir de allí se ubican los números ordenadamente en las 4 direcciones (arriba, abajo, derecha e izquierda).  A la recta horizontal se le llama eje x o de las abscisas; y la recta vertical se llama eje y o de las ordenadas.

En el eje x a la derecha están los números positivos.

En el eje x a la izquierda están los números negativos.

En el eje y arriba están los números positivos.

En el eje y abajo están los números negativos.

Para señalar la ubicación de un punto, debe hacerse con dos coordenadas que se escriben entre paréntesis: la primera corresponde a la coordenada del eje de las “x” (u horizontal) y la segunda, al eje de las “y” (o vertical).

El plano cartesiano queda de esta forma dividido en cuatro partes, que técnicamente reciben el nombre de “cuadrantes”. Reconocemos cuatro cuadrantes, que pueden apreciarse en la siguiente figura.

EJERCICIO:escribir las coordenadas para llegar al punto donde se encuentra el tesoro

Par Ordenado

Es una pareja de numeros  dados en cierto orden;  estudiaremos los pares ordenados numéricos; con  naturales, fracionarios y decimales.

♠ Concepto.-

(x, y) es un par ordenado cualquiera, x ≠ y, en donde x es el primer elemento llamado primera componente y y es el segundo elemento llamado segunda componente.

IMPORTANTE:  (x, y) ≠ (y, x).  Es decir el orden de las componentes no puede ser cambiado.

Estas componentes numéricas, se pueden graficar en los ejes cartesianos o plano cartesiano; la primera componente representa la abscisa y se ubica en el eje x; la segunda componente representa la ordenada y se ubica en el eje y. (x, y).

EJERCICIO:

1-)escribir los pares ordenados correspondientes a los puntos indicados en la siguiente figura

ESTADISTICA PARA 6-LA PROBABILIDAD

LA PROBABILIDAD

La probabilidad mide cuantitativamente el grado de certeza de que ocurra un suceso cuando se realiza un experimento aleatorio.

SUCESO:es cada uno de los posibles resultados que se pueden producir en una experiencia aleatoria.

CLASES DE SUCESOS

Suceso elemental: es cada uno de los elementos que forman parte del espacio muestral Ejemplo

1-Tirando un dado un suceso elemental es sacar 5.

Suceso compuesto:es cualquier subconjunto del espacio muestral.

Ejemplo

Tirando un dado un suceso compuesto sería:

1) Obtener numeros pares

2) obtener múltiplos de 3

3) Obtener numeros primos

ESPACIO MUESTRAL

En la teoría de probabilidades, el espacio muestral(E) consiste en el conjunto de todos los posibles resultados de un experimento aleatorio

EJEMPLO DE ESPACIO MUESTRAL EN EL LANZAMIENTO DE DOS DADOS 

E = 36

Ejemplo de espacio muestral en el lanzamiento de dos monedas

E = 4

EXPERIMENTO ALEATORIO

Son aquellos en los que no se puede predecir con certeza el resultado,de un suceso. ya que éste depende del azar.

Ejemplos:

1)Si lanzamos una moneda no sabemos con certeza cual sera el resultado

2-)Si lanzamos un dado tampoco podemos determinar el resultado que vamos a obtener.

3-)En general, todos los juegos de azar son aleatorios y sus resultados son impredecibles.

PROBABILIDAD Y RECTA NUMERICA

Suceso seguro o determinista: 

 está formado por todos los posibles resultados que se pueden obtener en un experimento aleatorio y se puede conocer con certeza su resultado anticipadamente, por ejemplo:

• 1)Al elegir al azar a una persona, esta tiene menos de 150 años
• 2)Al tirar una moneda, sale cara o sello
• 3)Al tirar un dado  sale un numero entre  1 y 6 
• 4)Es seguro que el agua empieza a hervir a los 100 Cº
• 5)Es seguro que el agua tiende a correr hacia el punto mas bajo...

Actividad 1 Sucesos seguros y sucesos imposibles Hay veces en que tenemos total seguridad de que un determinado suceso va a ocurrir necesariamente. Otras veces, tenemos la total seguridad que un determinado suceso no va a ocurrir bajo ninguna circunstancia. Pero en la mayor parte de los casos, el hecho que un cierto suceso ocurra es incierto. No tenemos seguridad de que va a ocurrir o que no va a ocurrir. Para poder caracterizar y analizar esta falta de certeza acerca de un determinado suceso, los matemáticos han introducido el concepto de probabilidad.En la siguiente lista de sucesos, marca con una S(seguro) aquellos que tú sabes que ocurrirán sin falta.Marca con la P(probable) y con la I(imposible)

a) Mañana voy a ir a la escuela ____ 

b)Dentro de una hora va a llover____

c)Son las 5:00 de la tarde y dentro de algunas horas va a anochecer _____

d)Mañana saldra el sol y nos iremos a pasear _____

e)Durante el dia es seguro que va a llover ____

f) Dentro de algunos años,tendre la misma edad que tuvo mi padre al morir ______

g) En el próximo Mundial de Fútbol el campeón será Chile ____

h)Si se lanza un dado, saldrá un número mayor que seis ____

EJERCICIOS

Métodos de medición de Probabilidad

Uno de los métodos más utilizados es aplicando la Regla de Laplace: define la probabilidad de un suceso como el cociente entre casos favorables y casos posibles.

NOTA:

Los casos favorables son los que cumplen con una o varias condiciones y los casos posibles son todos los que conforman el espacio muestral(E)

Ejemplos:

a) Probabilidad de que al lanzar un dado salga el número 2: el caso favorable (f) es tan sólo uno (que salga el dos), mientras que los casos posibles (n) son seis (puede salir cualquier número del uno al seis).

Por lo tanto:

b) Probabilidad de que al lanzar un dado salga un número par: en este caso los casos favorables (f) son tres (que salga el dos, el cuatro o el seis), mientras que los casos posibles (n) siguen siendo seis.

Por lo tanto:

c) Probabilidad de que al lanzar un dado salga un número menor que 5: en este caso tenemos cuatro casos favorables (f) (que salga el uno, el dos, el tres o el cuatro), frente a los seis casos posibles.

Por lo tanto: