universo matematico

lunes, 13 de noviembre de 2017

MATEMATICAS GRADO 7 - ECUACIONES LINEALES

Ecuaciones de primer grado


Una ecuación es una igualdad donde por lo menos hay un número desconocido, llamado incógnita o variable, y que se cumple para determinado valor numérico de dicha incógnita.
Se denominan ecuaciones lineales o de primer grado a las igualdades algebraicas con incógnitas cuyo exponente es 1 (elevadas a uno, que no se escribe).
Como procedimiento general para resolver ecuaciones enteras de primer grado se deben seguir los siguientes pasos:
1º Quitar paréntesis.
2º Quitar denominadores.
3º Agrupar los términos en x en un miembro y los términos independientes en el otro.
4º Reducir los términos semejantes.
5º Despejar la incógnita.
EJEMPLOS
Ecuación I.1: ecuación básica despejar

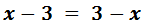
ecuaciones de primer grado resueltas
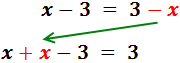
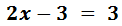
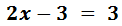
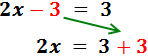
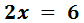
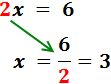
resolución de ecuaciones de primer grado paso a paso: ecuaciones simples, con fracciones, con paréntesis, con paréntesis dentro de otros, con signos negativos y ecuaciones sin soluciones o con infinitas soluciones
resolución de ecuaciones de primer grado paso a paso: ecuaciones simples, con fracciones, con paréntesis, con paréntesis dentro de otros, con signos negativos y ecuaciones sin soluciones o con infinitas soluciones
resolución de ecuaciones de primer grado paso a paso: ecuaciones simples, con fracciones, con paréntesis, con paréntesis dentro de otros, con signos negativos y ecuaciones sin soluciones o con infinitas soluciones

resolución de ecuaciones de primer grado paso a paso: ecuaciones simples, con fracciones, con paréntesis, con paréntesis dentro de otros, con signos negativos y ecuaciones sin soluciones o con infinitas soluciones

resolución de ecuaciones de primer grado paso a paso: ecuaciones simples, con fracciones, con paréntesis, con paréntesis dentro de otros, con signos negativos y ecuaciones sin soluciones o con infinitas soluciones

resolución de ecuaciones de primer grado paso a paso: ecuaciones simples, con fracciones, con paréntesis, con paréntesis dentro de otros, con signos negativos y ecuaciones sin soluciones o con infinitas soluciones

Simplificando queda que:

La solución de la ecuación es x = 3.

2. Agrupar términos

ecuación

Agrupamos los términos semejantes y los independientes, y sumamos:

ecuación



3. Quitar paréntesis

ecuación

Quitamos paréntesis:
ecuación

Agrupamos términos semejantes y sumamos

ecuación

Despejamos la incógnita y simplificamos

ecuación

4. Quitar denominadores
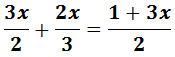
ecuaciones de primer grado resueltas
Quitamos denominadores, para ello en primer lugar hallamos el mínimo común múltiplo.
Tenemos varias formas de proceder con las fracciones:
  • a-)Sumar las fracciones de forma habitual.
  • b-)Multiplicar la ecuación por el mínimo común múltiplo de los denominadores.
En esta ecuación aplicaremos la segunda opción. De este modo los denominadores van a desaparecer.
Multiplicamos la ecuacion  por m.c.m.(2, 3) = 6:


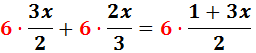
resolución de ecuaciones de primer grado paso a paso: ecuaciones simples, con fracciones, con paréntesis, con paréntesis dentro de otros, con signos negativos y ecuaciones sin soluciones o con infinitas soluciones

Multiplicando y simplificando queda:

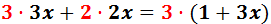
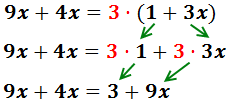
resolución de ecuaciones de primer grado paso a paso: ecuaciones simples, con fracciones, con paréntesis, con paréntesis dentro de otros, con signos negativos y ecuaciones sin soluciones o con infinitas soluciones

resolución de ecuaciones de primer grado paso a paso: ecuaciones simples, con fracciones, con paréntesis, con paréntesis dentro de otros, con signos negativos y ecuaciones sin soluciones o con infinitas soluciones

Pasamos las x’s a la izquierda:


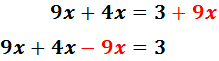
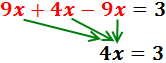
resolución de ecuaciones de primer grado paso a paso: ecuaciones simples, con fracciones, con paréntesis, con paréntesis dentro de otros, con signos negativos y ecuaciones sin soluciones o con infinitas soluciones


resolución de ecuaciones de primer grado paso a paso: ecuaciones simples, con fracciones, con paréntesis, con paréntesis dentro de otros, con signos negativos y ecuaciones sin soluciones o con infinitas soluciones
Finalmente, el coeficiente de la X  pasa dividiendo al otro lado:

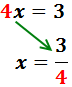
resolución de ecuaciones de primer grado paso a paso: ecuaciones simples, con fracciones, con paréntesis, con paréntesis dentro de otros, con signos negativos y ecuaciones sin soluciones o con infinitas soluciones

La solución de la ecuación es x = 3/4 y no se puede simplificar 


5. Quitar paréntesis y denominadores

ecuación
Quitamos paréntesis multiplicando de la manera habitual y simplificamos:




ecuación 

Quitamos denominadores,la segunda ecuacion se multiplica por 2 agrupamos y sumamos los términos semejantes:

ecuación

https://www.vitutor.com/ecuaciones/1/ecuaciones.html

NOTA: A CONTINUACION DEJO EL LINK PARA COMPLEMENTAR LA CLASE DE ECUACIONES CON UN VIDEO 

https://youtu.be/T3HeX5Fi1oY


EJERCICIOS PARA RESOLVER

ecuaciones_en_q08
http://www.profesorenlinea.cl/matematica/EcuacioEjercicios.htm






Publicado por en 20 comentarios:
Etiquetas: ,

domingo, 5 de noviembre de 2017

GEOMETRIA GRADO 6 y 7 - CUERPOS GEOMETRICOS

Cuerpos geométricos: conceptos básicos

https://www.portaleducativo.net/primero-basico/110/Cuerpos-geometricos-conceptosbasicos

1- ¿Qué son los cuerpos geométricos?
Un Sólido o Cuerpo Geométrico es una figura geométrica de tres dimensiones (largo, ancho y alto), que ocupa un lugar en el espacio y en consecuencia tiene un volumen


Los cuerpos geométricos pueden ser:

Poliedros :Son sólidos geométricos de muchas caras, que contienen los siguientes elementos: caras, aristas, vértices.



poliedors


ttps://www.portaleducativo.net/primero-basico/110/Cuerpos-geometricos-conceptosbasicos

2.1- Caras
Son las superficies planas que forman el poliedro, las cuales se interceptan entre sí.



caras

ttps://www.portaleducativo.net/primero-basico/110/Cuerpos-geometricos-conceptosbasicos
2.2- Aristas
Son los segmentos formados por la intersección de dos (2) caras.


aristas


https://www.portaleducativo.net/primero-basico/110/Cuerpos-geometricos-conceptosbasicos
3- Cuerpos redondos

Son cuerpos geométricos compuestos total o parcialmente por figuras geométricas curvas; como por ejemplo el cilindro, la esfera o el cono.



Cuerpos redondos
https://www.portaleducativo.net/primero-basico/110/Cuerpos-geometricos-conceptosbasicos


3.1- Reconozcamos los cuerpos redondos en nuestro entorno
En nuestro entorno podemos encontrar muchas formas.¿Reconoces alguna?
Recuerda que los cuerpos redondos tienen superficies curvas.
Algunos ejemplos que podemos encontrar en nuestro entorno son:


 cono


cilindro

esfera
https://www.portaleducativo.net/primero-basico/110/Cuerpos-geometricos-conceptosbasicos
NOTA:
Las superficies curvas, ya sea del cilindro, cono o esfera, son consideradas igualmente caras. Por lo tanto el cilindro, por ejemplo, tiene dos caras planas,una base y una superior  y una cara lateral curva. El cono tiene una cara  plana  superior y una cara curva. La esfera tiene una cara curva.


ACTIVIDAD DE RECUPERACION:

1-) Dibujar en una cartulina los diferentes cuerpos rfedondos y su relacion con el entorno

2-) Con material reciclable construir un cuerpo geometrico tridimensional,que puede ser un poliedro o un cuerpo redondo.














Cuerpos Redondos
Publicado por en 3 comentarios:
Etiquetas: ,
Suscribirse a: Entradas (Atom)